No Products in the Cart
Día a día, los técnicos que se desempeñan en labores de acceso por cuerdas, se ven enfrentados a varios desafíos, uno de ellos es ¿Dónde instalar las cuerdas?... de las que se suspenderán.
Nuestra legislación es amplia y ambigua, pero vaga en algunos aspectos, por ejemplo, al darnos la directriz de instalar en condiciones y elementos que resistan una carga mínima de 22KN, no considera otros aspectos tales como distancia de caída en cuerdas (tema para otra ocasión), o cómo distribuiremos las cargas en los anclajes desde donde se realizará la suspensión.
Muchas veces, se ha visto que por lógica o deducción se realizan instalaciones a puntos determinados, ya sean chapas o similares, en los cuales se “juega” con los ángulos, aprovechando esto para tener la dirección de una determinada “bajada”. Justamente allí, es donde nace el triángulo de fuerza y distintas preguntas: ¿Sabemos el fundamento del triángulo? ¿Es necesario triangular las cargas? Siempre que instalemos cuerdas, vamos a generar un ángulo de trabajo al momento de montarla, y es necesario conocerlos y utilizarlos de buena manera para poder trabajar de manera más segura.
La experiencia nos indica que mientras sea mayor el ángulo, mayor carga recibirán los anclajes, por el contrario, cuando tenemos 0° en el ángulo (solo posible teóricamente, ya que siempre habrá una separación mínima), se recibirá la mitad de la fuerza que se esta generando en la carga.

Para ello, debemos revisar la siguiente formula: F’=F/2/cos X.
Lo explicaremos de la mejor forma posible.👇
F’ será la fuerza aplicada en cada anclaje, F será la fuerza aplicada al triángulo de fuerzas (la carga) y X es el ángulo formado respecto a la vertical (esto será el ángulo completo dividido en 2) En palabras más matemáticas:
'La fuerza generada es igual a la mitad de la carga suspendida partido por el coseno del ángulo respecto a la vertical del triángulo.' Pero no nos confundamos con esta última frase 😓 , veamos un par de ejemplos para comprender mejor, la fórmula planteada. 😏

En la figura superior, vemos que F son 100 N, el ángulo es de 60° por lo tanto X seria 30°. Ahora desarrollemos👇:

De esta forma nos damos cuenta que la fuerza aplicada en cada anclaje con una carga de 100 Newton sería de 58 Newton en cada uno.

En ejemplo superior, vemos que F son 100 N, el ángulo es de 120° por lo tanto X sería 60°. Ahora desarrollemos:
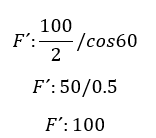
Y desde aquí empiezan nuestros problemas 🤦, no podemos superar este ángulo, ya que si lo hacemos estaríamos traspasando toda la carga a cada uno de los anclajes, aumentando exponencial el factor de riesgo.
Por lo tanto, como conclusión podemos decir que, hasta los 60° tenemos un factor aceptable, y que a partir de los 120° en vez de beneficiarnos de la distribución de carga pasamos a realizar justo lo contrario de lo que queremos. 💀
Entendido lo anterior, nos preguntamos:
Triángulo bloqueado: Es común verlo en las “reuniones” de escalada, ya que cuando no varía su dirección se genera una distribución óptima de la fuerza que reciben los anclajes.
Si la dirección cambia❗, inmediatamente, uno de los brazos recibe menos tensión que el otro, pudiendo esto generar algún problema, pero que, si es bien contemplado y valorizado, puede ser una ventaja ya que al fallar la carga pasaría suavemente al otro brazo sin aumentar carga en dicho anclaje. Lo mejor para este tipo de anclaje es el ocho de doble presilla (ocho dobles, oreja de conejo🐰 u otro nombre similar) u otros similares.

Triángulo dinámico: A diferencia del anterior, los brazos del triángulo siguen recibiendo la misma tensión aún cuando se cambie la dirección. Favorecidos por esto, se ajustará en el sentido de la carga. Lo que puede significar un problema, ya que si falla se puede tensionar de forma brusca, puede generar cargas al ajustarse y terminar sobrecargando el sistema.

Si bien es cierto, los cálculos son engorrosos, o difíciles de dilucidar, los ángulos en la práctica, solo con tu celular y un par de aplicaciones podrás darte cuenta que se puede ajustar de una forma más técnica y profesional tu trabajo.
Al momento de instalar tus cuerdas y la aplicación Angulus, basta solo una foto para ver el ángulo de trabajo del triángulo. A eso le sumamos la calculadora del mismo celular con la formula expuesta, y bueno, sería todo para ver que estamos reduciendo los riesgos en el trabajo que realizamos. Esto también nos podría ayudar a ejecutar y desarrollar nuestros procedimientos de trabajo.